Практически
все слышали выражение «цифровое управление» и «цифровое устройство».
Почти все знают,
что практически все современные устройства, начиная от бытовых музыкальных
центров, телевизоров или стиральных машин и заканчивая сложнейшими космическими
кораблями и искусственными спутниками земли состоят из одиночных микросхем или
некоторого их количества.
Некоторым
также известно, что микросхемы бывают разные – микропроцессоры,
микроконтроллеры, логика, интерфейсные схемы и т.д. и т.п.
Программисты и
разработчики знают, какие разновидности микросхем и процессоров бывают, какую
архитектуру они имеют, как программируются и т.п.
Но далеко не
все знают и понимают, как они устроены внутри, как и из чего они состоят и создаются.
И речь идёт не об обобщённой грубо-примитивной функциональной схеме из даташита
на ту или иную микросхему, а о том, что кроется за всем известными кубиками
типа ALU, REGISTERS, ADC, стрелочками
между ними и пр. Сказать что это –
арифметико-логическое устройство, регистры, АЦП и т.д. – по сути, не сказать
ничего.
Здесь будут описаны
общие вопросы синтеза и устройства цифровых устройств на базе простейших
логических микросхем типа широко известных и распространённых отечественных
К155 (либо их многочисленных аналогах), а также
некоторые основы микропроцессорной техники и вопросы сопряжения цифровых и
аналоговых схем.
Хотелось бы
отметить, что:
1. Практически все цифровые микросхемы и устройства могут быть
синтезированы их простейших логических элементов. Исключение составляют
«составные» аналого-цифровые схемы типа АЦП, аналоговых мультиплексоров, различных
декодеров и пр. Такие схемы будут рассмотрены частично, без подробного анализа
их аналоговых узлов.
2. Некоторые (в основном глубоко теоретические) аспекты синтеза и
функционирования схем опущены либо упрощены. Это сделано сознательно, т.к. это
очень обширные вопросы, на полное изучение которых в специализированных учебных
заведениях отводится немало часов лекций и различных практических занятий.
Более того, существует немало смежных тем, которые напрямую к синтезу не
относятся, но без чёткого понимания которых тяжело что-либо сделать. К примеру,
чтобы спроектировать аппаратный умножитель чисел, необходимо не лишь уметь
синтезировать схемы, но ещё и знать алгоритмы умножения как такового.
3. Быстродействие устройств, синтезированных на обычных лог. элементах
обычно невелико.
4. Простейшие логические элементы, типа инверторов, И, ИЛИ и пр. создаются
из обычных дискретных элементов (диоды, транзисторы, резисторы). Вопросы их
проектирования рассматриваться не будут, т.к. практической пользы от этого
мало. Кроме того, в них нередко применяются некоторые «экзотические» детали (наиболее
яркий пример – многоэмиттерные транзисторы), которые в дискретном исполнении вообще
не выпускаются.
5. Почти во всех примерах статьи присутствует некоторые «практический
уклон», т.е. те или иные рекомендации даются с учётом характеристик реальных
микросхем. Т.о. данная статья не является 100% лекцией или «примерами» для
студентов, когда те или иные задания или схемы часто лишены какого-то
практического смысла и направлены лишь на усвояемость той или иной части
лекционного материала.
6. Может показаться, что в наше время синтез каких-либо сложных устройств
на базе примитивных лог. элементов, триггеров и счётчиков полностью себя изжил.
Да, действительно, любой микроконтроллер окажется намного дешевле, а схема с
его использованием гораздо быстрее, компактнее и надёжнее, нежели гора 155-х
микросхем и сопутствующих им деталей, реализующих те же действия. Но, в то же
время, существует немало задач, где простые логические схемы выглядят гораздо
логичнее, понятнее и работают быстрее каких-либо сложных микропроцессорных
структур. Кроме того, современные, широко применяемые в настоящее время
микросхемы программируемой логики ПЛИС являются ни чем иным, как «набором»
различных практически дискретных логических элементов и триггеров. Для
полноценного использования таких микросхем необходимо в том числе чётко знать и
понимать различные подходы и аспекты синтеза цифровых схем.
7. При чтении данной статьи рекомендуется держать под руками какой-нибудь
справочник по микросхемам, например, [1].
8. Следует также отметить, что здесь почти не рассматриваются практические аспекты
конструирования устройств на базе тех или иных микросхем, они обычно неплохо
освещаются в литературе (в той же [1], например) и в
статьях в интернете.
9. Подавляющее большинство приведенных здесь схем являются чисто
иллюстративными. Потому для их реального воплощения «в железе» может
потребоваться некоторая доработка (например, определение номиналов деталей,
приведение к реально производящимся типам микросхем, какое-то согласование и
т.д.).
10. Все предлагаемые в этой статье описания и подходы к синтезу схем и
блоков не являются чем-то новым, они многократно описаны в различных учебниках для
ВУЗов соответствующей направленности и различных университетских лекциях и
методичках для студентов, которые можно найти в интернете. Но, по мнению автора
все они, как, в принципе любое учебное пособие, перегружены массой
разнообразного теоретического материала и часто привязаны к конкретным учебным
программам того или иного ВУЗа. Кроме того, в них крайне мало практической
информации и «переходов» от сугубо теоретических схем к их реализациям на базе промышленно
выпускаемых микросхем. А университетские «раздробленность» и «разбросанность»
материала по разным дисциплинам и курсам сильно затрудняют его понимание. Потому,
в таких условиях часто возникает ситуация «за деревьями леса не видно».
В силу значительной
«обширности темы», повествование разделено на части:
1. Базовые
понятия и основные узлы цифровых схем.
2. Промышленно выпускаемые простейшие цифровые схемы.
3. Управляющие автоматы. Принцип микропрограммного управления.
4. Устройство и разработка цифровых вычислительных систем.
5. Сопряжение цифровых и аналоговых схем. Аналого-цифровые
устройства.
Часть 1. Базовые
понятия и основные узлы цифровых схем
Терминология
Уровень
сигнала – напряжение на входе или выходе схемы. В подавляющем большинстве
случаев измеряется относительно земли.
Цифровые схемы
всегда оперируют двоичными сигналами, т.е. такими, в которых присутствуют
2 ярковыраженных уровня (отсюда и название – двоичный сигнал). Эти уровни
называют логическим нулём (низкое напряжение) и логической единицей (высокое напряжение). Все остальные уровни являются «нерабочими». Поведение
цифровых схем на таких уровнях обычно не описывается и в ряде случаев может
оказаться нестабильным. Потому, этого следует избегать.
Конкретные
напряжения лог. нуля/единицы зависят от схемотехники цифровых элементов и могут
отличаться для разных семейств микросхем. Чаще всего это 0в (лог. 0) и +Uпитания (лог. 1). На практике вводится понятие порога
срабатывания – некоего напряжения, уровень сигнала выше которого считается
лог. 1, ниже – лог. 0.
Очень
распространено понятие «уровни ТТЛ». ТТЛ – аббревиатура от
«транзисторно-транзисторная логика». Это один из видов внутренней схемотехники
цифровых логических элементов и схем. Широко известные отечественные серии
микросхем К155, К555 и пр. – ТТЛ схемы. Уровни ТТЛ: лог. 0 – 0в, лог. 1 — +5в.
Порог – в среднем +1.4 в, у разных серий микросхем немного отличается. Потому,
по факту, если на входе 0..+1.4в – это лог. 0, а +1.4в .. +5в – лог. 1. Понятие
«напряжение» в цифровой технике упоминается достаточно редко.
Сразу отметим,
что большинство современных схем хоть и не являются ТТЛ схемами, но, работают с
уровнями напряжений ТТЛ. Благодаря этому, очень редко возникают какие-либо
проблемы согласования разных цифровых схем по напряжению. Более подробно – см.
часть 5, раздел 5.5 .
Рассмотрим структуру
двоичного периодического сигнала – рис. 1.
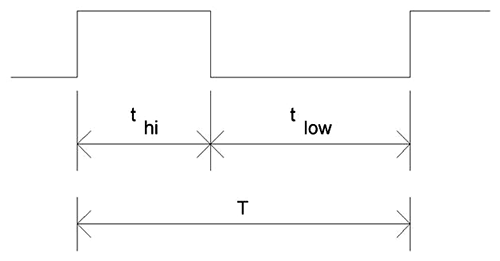
Рис. 1. Двоичный
периодический сигнал.
На рис. 1:
— T – период – время через которое сигнал начинает повторяться.
Частота сигнала F=1/T.
— thi — длительность
верхней полочки (высокого уровня) сигнала.
— tlow — длительность
нижней полочки (низкого уровня) сигнала.
Соотношение thi /T называется
скважностью импульса. Это очень важное понятие, широко применяется в различных
системах управления. Тактовые сигналы цифровых схем обычно имеют скважность
0.5, т.е. у них длительности высокого и низкого уровней в каждом периоде равны.
Сигнал со скважностью, равной 1 – это просто лог. 1, скважность, равная 0 –
лог. 0.
Направление
тока в цифровых цепях обычно не рассматривается. Оно не зависит от направления
распространения информации и зависит лишь от лог. уровня на выходе элемента и
того узла, к которому этот выход подключен. Более подробно мы рассмотрим это в
5-й части.
Обозначение
типов входов и выходов цифровых элементов/микросхем
Внутренняя
схемотехника логических элементов в этом цикле статей рассматриваться не будет,
рассмотрим лишь существующие типы логических выходов элементов, т.к. в схемах
часто учитываются и сознательно используются те или иные особенности.
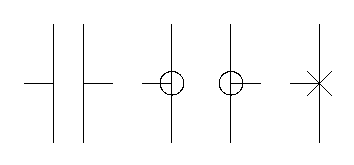
а)
б) в) г)
д)
Рис.2 Обозначения
входов-выходов
На рис. 2:
а) обычный (прямой) вход;
б) обычный (прямой) выход;
в) инверсный вход;
г) инверсный выход;
д) входы питания либо входы подключения
кварцевых резонаторов.
Инверсные
входы/выходы широко используются в более сложных схемах – мультиплексоры,
дешифраторы и т.д. и т.п., а также в микропроцессорной технике.
Существует 3
типа логических выходов: обычный, с открытым коллектором и с Z состоянием.
«Выход с
открытым коллектором». Означает, что на выходном транзисторе отсутствует
нагрузочный резистор в цепи коллектора – рис. 3-б. На рис. 3-а приведена
примерная схема обычного выхода.
Иногда
называют – выход с ОК.
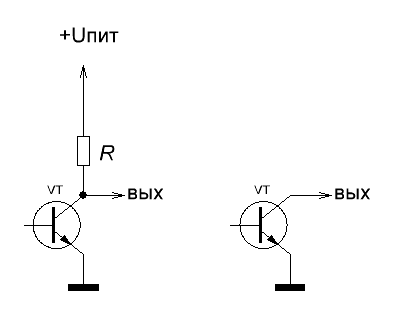
а)
б)
Рис. 3. Обычный выход
и выход с ОК
Когда
транзистор закрыт, на выходе лог. 1 (Uпит), в случае с
ОК – обрыв.
Когда открыт,
это лог. 0 – на выходе практически потенциал земли в обоих случаях.
Выход с ОК
можно использовать для согласования узлов – получения на нём какого-то другого
напряжения лог. 1. К примеру, +3.3в с целью согласования с соответствующими
узлами. Более подробно мы рассмотрим это в части 5.
В последнее
время применяются не биполярные транзисторы, а полевые, но суть и логика работы
от этого совершенно не меняется. Единственное отличие в терминологии – здесь
уже не ОК, а открытый сток (ОС).
Резистор между +Uпит и выходом называют подтягивающим (pull-up). Если резистор находится между землей и ногой элемента
(применяется на входах для гарантированного получения лог. 0), то он называется
притягивающим (pull-down).
«Третье
состояние выхода», оно же «Z-состояние» выхода.
Выход схемы с возможностью перехода в такое состояние называют «тристабильным
выходом». Это понятие применяется лишь к выходам схем и под ним имеется в
виду не какое-то напряжение на выходе элемента, как может показаться на первый
взгляд. Это просто обрыв, т.е. в этом состоянии выход «висит в воздухе», он
фактически отключен от схемы узла, к которому относится.
Практический
смысл и применение этой возможности будет рассмотрен ниже – п. 4.6 раздела 4
этой части.
«Выход с
повышенной нагрузочной способностью» имеет выходной транзистор повышенной
мощности. По напряжению такой выход ничем не отличается от обычного, но
способен выдерживать гораздо большие нагрузки. Часто всегда такие выходы
являются ещё и с ОК.
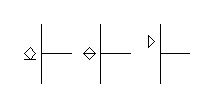
а)
б) в)
Рис. 4. Графические
обозначения выходов с ОК (а), Z состоянием (б) и с
повышенной нагрузочной способностью (в).
Бит – неделимая
единица информации. Может принимать значения 0 и 1. По сути можно сказать, что
бит – один двоичный сигнал. Понятие бита применяется очень часто, особенно в
вычислительной технике и в процессорах. Иногда бит называют разрядом. Т.е.
выражения «8-битный» и «8-разрядный» — совершенно одно и то же.
Тетрада – единица
информации, равная 4 битам.
Байт –
единица информации, равная 8 битам.
Слово –
4 байта.
Двойное
слово – 4 байта.
Эти понятия также
очень широко применяются в вычислительной технике
Нагрузочная
способность – в общем понимании это ток, который может обеспечить тот или
иной элемент схемы на своём выходе.
В ряде
случаев, когда в схеме используются лог. элементы одного типа (например, лишь
микросхемы 155 серии), возможна трансформация данного понятия в кол-во входов,
которые можно одновременно подключить к выходу элемента.
КЛС или КС – комбинационная (логическая) схема. Это схема, состояние всех
выходов которой в момент времени t зависит лишь от состояния
её входов в тот же момент времени t. Т.е. никакой
памятью и зависимостями входов от её же выходов такая схема не обладает.
Состоит обычно из простых логических элементов, либо каких-то более сложных
узлов на их основе.
Быстродействие
КС – время, за которое изменение состояний входных сигналов отражается на
состоянии выходных. Это время ещё называют временем срабатывания схемы. Оно обычно
равно сумме времён срабатывания всех лог. элементов в самой длинной цепочке
лог. элементов. Т.о. чем больше элементов участвует в выработке того или иного
выходного сигнала схемы, тем меньше её быстродействие.
Триггер – КС, обладающая памятью. Иными словами, состояние выходов в момент времени t может зависеть от их же состояния в момент времени t-1. Такие КС всегда имеют обратные связи. Т.е. ряд её
выходов подаются на её же входы.
Особенностью
любых триггеров является то, что они способны хранить информацию лишь во включённом
состоянии. При обесточивании схемы они «забывают» то, что в них было записано.
Существуют разные типы триггеров, они рассмотрены ниже.
Все прочие
узлы – мультиплексоры, демультиплексоры, дешифраторы, микросхемы памяти (в т.ч.
простые регистры), счётчики и т.д. и т.п. – синтезируемые схемы, являются сочетаниями
КС и триггеров.
Шина – набор
однотипных (сходных) по функциональному назначению сигналов (проводников). К примеру,
шина данных (ШД) – сигналы, по которым то или иное
устройство получает данные. Часто используется понятие разрядность шины –
кол-во одиночных сигналов в ней.
Временная
диаграмма – график изменения сигналов на входах-выходах схемы с течением
времени. К примеру – рис. 5.
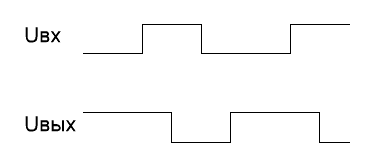
а)
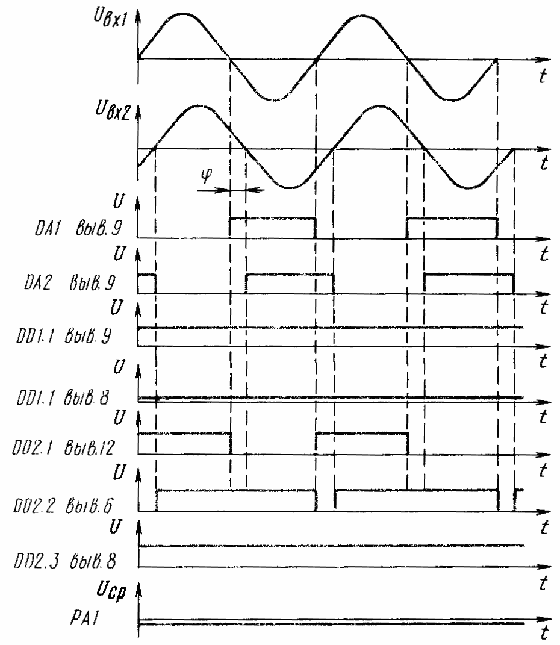
б)
Рис. 5. Примеры
временных диаграмм
Целью
построения подобных диаграмм – иллюстрация работы какого-либо узла, либо
микросхемы в целом. На одной диаграмме допускается совмещать сигналы с разных
элементов схемы, разнородные сигналы и типы выводов. Т.е. можно рисовать и аналоговые
и цифровые выводы, входы и выходы и т.д.
Способы передачи
информации в цифровых схемах
Т.к. вся
информация в цифровых схемах всегда представляется в виде двоичных сигналов, то
встаёт вопрос – каким образом можно передать те или иные данные по каналам
связи. Ведь даже двоичные данные можно передать по-разному. Рассмотрим основные
способы представления и передачи двоичных данных.
1. Параллельный
код. Это наиболее простой и очевидный способ. Все процессоры выдают данные
в параллельном коде. Данные представляются в виде каких-то «элементарных»
блоков (тетрада, байт, …) и эти блоки передаются по очереди и отдельно друг от
друга. Все биты блока передаются одновременно, т.е. параллельно.
2. Последовательный
код. Биты данных передаются последовательно по одному физическому проводу.
Соответственно существует 2 подвида передачи – младшими битами вперёд и
старшими вперёд.
Для передачи данных,
кроме самих сигналов данных, часто нужно передавать ещё, как минимум 2 управляющих
сигнала – строб (синхронизация) и подтверждение. Стробом передатчик «говорит»
приёмнику о наличии на шине новой порции данных, а подтверждение посылается
приёмником для сообщения того, что он принял данные. В ряде случаев один из
этих сигналов может отсутствовать, а также могут дополнительно посылаться
какие-то доп. сигналы (готовность приёмника к приёму, направление передачи и
пр.).
Как можно
заметить, параллельный код наиболее скоростной – за каждый такт мы можем
передать сразу несколько битов данных, в то время как в последовательном коде
мы передаём лишь один бит за один такт. Но, на практике, в реальных
каналах связи в подавляющем большинстве случаев используется последовательное
кодирование.
Существует
очень много подвидов последовательной передачи данных, их кодирования с целью
улучшения помехозащиты и пр. Мы не будем рассматривать здесь все эти аспекты.
Логические
операции
Логические
операции – это некий аналог операций арифметики, т.е. набор простейших «базовых»
операций над двоичными аргументами. Этот набор включает в себя всего 3
операции:
— ИЛИ (логическое сложение, OR). Обозначается как y=x1 v x2. Для простоты записи иногда пишут y=x1+x2.
Внимание! Знак ‘+’ здесь — это не
привычное математическое сложение. В языках программирования используется
вариант записи y=x1|x2. Результат операции ИЛИ равен 1,
если все операнды равны 1 либо вместе, либо по одному.
Таблица
истинности (ТИ) для 2-х операндов выглядит так:
x1
x2
Y
0
0
0
0
1
1
1
0
1
1
1
1
Свойства операции OR: x v 1 = 1; x v 0 = x; x v x = x; x1 v x2 = x2 v x1.
— И (логическое умножение, AND); y= x1 ^ x2 = x1 & x2 = x1x2. Результат равен 1, если все
операнды одновременно равны 1. Таблица истинности:
x1
x2
Y
0
0
0
0
1
0
1
0
0
1
1
1
Свойства: x^1=x; x^0=0; x^x=x; x1^x2=x2^x1.
— НЕ (отрицание, NOT). Гораздо чаще применяется название
«инверсия». Обозначение: y==~x. Результат равен 1, когда x=0 и
наоборот.
Таблица
истинности:
x1
y
0
1
1
0
Операции в
порядке убывания приоритета: НЕ, И, ИЛИ. Как и в обычной матеметике, для
изменения приоритета используются скобки.
Иногда к числу
основных причисляют и операцию XOR – исключающее ИЛИ — 
. Результат равен 1, когда лишь один
из операндов равен 1.
Таблица
истинности (ТИ):
x1
x2
Y
0
0
0
0
1
1
1
0
1
1
1
0
По мнению
автора она не является базовой, т.к. может быть синтезирована из 3-х базовых
операций (пример приведён ниже, в разделе 1), а причина считать её базовой лежит
в том, что она реализована в составе промышленно выпускаемых микросхем логики
наряду со всеми остальными операциями. Потому на практике её не нужно
синтезировать, можно взять готовый элемент.
Все 4 операции
всегда однобитовые, даже если выполнять их над многоразрядными операндами, то
любой бит любого операнда обрабатывается совершенно независимо от остальных и
независимо от результатов, полученных над другими битами.
Промышленностью
выпускаются лог. элементы, реализующие эти операции над другим кол-вом
операндов (3, 4, 8) и элементы, содержащие не одну лог. операцию, а несколько.
Наиболее часто
встречаются элементы И-НЕ, ИЛИ-НЕ, в которых результат операций И, ИЛИ
дополнительно инвертируется. Такие элементы могут использоваться как простые
инверторы (см. свойства операций И, ИЛИ).
Кол-во входов
элемента обозначают цифрой: 2И – 2-хвходовый элемент, 3ИЛИ – 3-хвходовый
элемент ИЛИ и т.д.
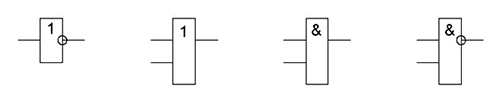
а)
б)
в) г)
Рис. 6. УГО
логических элементов
На рис. 6
приведены условные графические обозначения лог. элементов, реализующих функции
инвертора (а), ИЛИ (б), И (в). Рис. 6-г иллюстрирует обозначение составного
элемента И-НЕ.
Логические
тождества
Как и для
обычных арифметических операций, для логических тоже существует
ряд тождественных преобразований. Приведём некоторые из них.
Согласно этим
тождествам всегда можно заменить операцию И на операцию ИЛИ и наоборот. Иногда
применяются выражения типа «реализовать в базисе И-НЕ» или «реализовать в
базисе ИЛИ-НЕ». Смысл прост – использовать лишь указанные операции.
Базис И или
базис ИЛИ нереализуемы, т.к. всегда необходима инверсия. Полностью отказаться
от инверсии невозможно.
На практике к
выбору лишь одного (любого) базиса следует относиться осторожно – изначально
относительно простое выражение (и, как следствие, схема его реализующая) может
«раздуться» до больших размеров. Соответственно, неизбежно уменьшение
быстродействия.
Тождества
справедливы для любого числа аргументов.
Раздел 1.
Синтез КС
КС встречаются
очень часто. Они являются неотъемлемой частью любого устройства, начиная от примитивной
ёлочной гирлянды и заканчивая сложнейшими микропроцессорами. К примеру, арифметико-логическое
устройство (АЛУ) любого процессора на 90% — комбинационная схема.
Функционирование
любой КС можно описать несколькими способами. Чаще всего используются формулы и
таблицы истинности (ТИ).
Синтезировать
КС можно непосредственно по таблице истинности, но во многих случаях удобнее и
нагляднее использовать карты Карно (они же диаграммы Вейча). Карты Карно также
позволяют минимизировать (упростить) конечные выражения и схемы.
Рассмотрим синтез
на примере элемента «исключающее ИЛИ». Конечно, такие элементы существуют в
готовом виде, в составе микросхем логики, но этот простой пример поможет
понять, как ТИ и карты Карно используются при синтезе схем.
Формула и таблица
истинности были приведены выше.
Для искл. ИЛИ
карта Карно имеет вид – рис. 7.
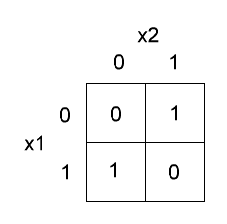
Рис 7. Карта Карно
для операции XOR
Из карты
видно, что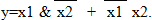 
Такая же формула получится и из таблицы истинности.
А это
выражение уже очень легко реализуется на логических элементах – рис. 8.
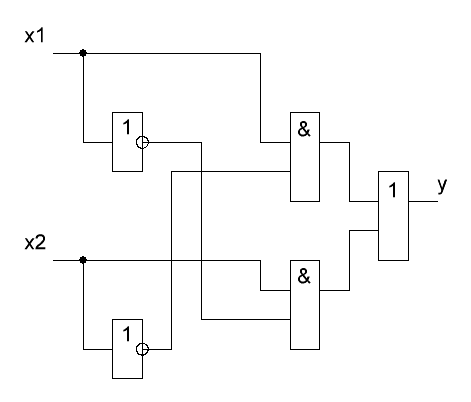
Рис. 8-а. Схема
элемента «Искл. ИЛИ» на
элементах И, ИЛИ, НЕ
Используя
вышеприведенные тождества, можно реализовать данную
схему, например, в базисе И-НЕ:
Рис. 8-б. Схема
элемента «Искл. ИЛИ» на
элементах И-НЕ (в базисе И-НЕ)
В этом
конкретном случае сложность схемы не изменилась, но, применительно к реальным
микросхемам, её характеристики ухудшились – ко входам этого узла здесь
подключены не 2 входа, как на рис. 8-б, а 3. Следовательно, каждый вход схемы
сильнее нагружает выходы элементов, к которым он подключается. Перегрузка
выходов может привести к выгоранию выходных каскадов элемента и к порче всей
схемы в целом.
В данном
случае этот недостаток можно устранить подачей лог. 1 на один из входов каждого
из входных элементов И-НЕ. Можно также использовать специальные повторители
сигнала – элементы, реализующие функцию y=x.
Подобные
нюансы всегда следует учитывать при разработке схем, особенно, если в них
применяются микросхемы различных типов.
Рассмотрим синтез
одноразрядного арифметического сумматора – узла, который является неотъемлемой
составной частью любого микропроцессора или микроконтроллера.
Таблица
истинности сумматора:
Входной перенос, p
Слагаемое 1, a
Слагаемое 2, b
Сумма, S
Выходной
перенос, P
0
0
0
0
0
0
0
1
1
0
0
1
0
1
0
0
1
1
0
1
1
0
0
1
0
1
0
1
0
1
1
1
0
0
1
1
1
1
1
1
Сумматор можно
синтезировать 2-мя способами:
Способ
1. Универсальный
Сумматор, как
и любая «многовыходовая» КС синтезируется по частям – каждый выход по
отдельности.
Карта Карно
для выхода S – рис 9.
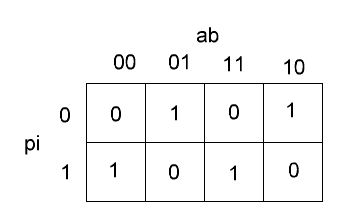
Рис. 9. Карта Карно для выхода S сумматора
Формула: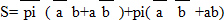 
Карта Карно
для выхода P – рис. 10.
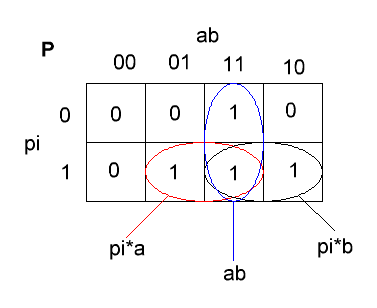
Рис. 10. Карта Карно для выхода P сумматора
Формула: P = ab + pia + pib = ab + pi(a+b)
Рис. 10
иллюстрирует основную цель построения подобных карт — минимизация логических
выражений.
Ряд важных
особенностей карт Карно:
1. Карту всегда необходимо строить так, чтобы любым 2-м смежным клеткам
соответствовало изменение лишь одной (любой) входной переменной. Именно поэтому
в верхней строчке используется очерёдность 00, 01, 11, 10, а не 00, 01, 10, 11
– во втором случае получаются соседние значения 01, 10 – меняются обе цифры –
это неверно.
2. Овалами обозначены т.н. «склейки» — области карты, где значение
выходного сигнала (содержимое клетки) не зависит от одной или нескольких входных
переменных. Так, в красном овале выходной сигнал P не зависит от сигнала b, в чёрном не зависит от сигнала a,
а в синем не зависит от pi. Склейки показывают, что в этих
случаях тот или иной сигнал можно не учитывать, что упрощает (минимизирует)
схему. На карте рис. 7 нет единиц, находящихся в смежных клетках, поэтому там
нельзя ничего склеить (минимизировать) и приходится реализовывать все единицы
как есть, с учётом всех входных сигналов.
3. Склеивать и учитывать при составлении формулы следует лишь клетки, где
выходной сигнал равен 1.
4. Неопределённые сигналы (*) можно склеивать с чем угодно.
Имея формулы
для сигналов S и P можно легко
нарисовать схемы, реализующие эти сигналы.
Способ
2.
Анализируя
таблицу истинности сумматора, можно заметить, что сигнал S в
первых 4 строках (выделены жирным) – реализует исключающее ИЛИ над входными сигналами a и b, а сигнал P – лог. И над этими же сигналами. На основании этого без
каких-либо карт и минимизаций можно составить схему т.н. двоичного
полусумматора – рис. 11.
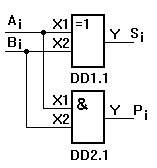
Рис. 11. Двоичный
полусумматор
Из 2-х таких полусумматоров
и элемента ИЛИ получается полный сумматор – рис. 12.
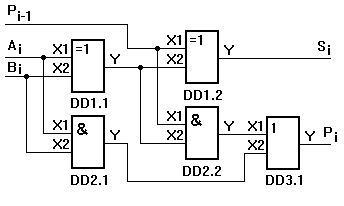
Рис. 12. Полный одноразрядный двоичный сумматор на элементах
исключающее ИЛИ, И
В итоге такая
схема проще (и чаще быстрее), нежели та, которая получится при общем синтезе.
Но такой способ применим не всегда.
Раздел 2.
Триггеры
Как уже был сказано
выше, триггер это КС, состояние выходов которой зависит не лишь от входных
сигналов, но и от её же собственных выходных.
Обычно
триггеры имеют несколько входов и 2 выхода – прямой и инверсный, т.е. всегда
находятся с противофазе друг другу. Иногда один из выход отсутствует, но у
одиночных триггеров это встречается достаточно редко. Набор входов разный у
разных типов триггеров. Выходы триггера обычно называют Q и Q.
По способу
записи информации триггеры разделяются на асинхронные и синхронные.
Асинхронные
триггеры меняют своё состояние сразу же после поступления информационных
сигналов на их входы.
Синхронные
триггеры реагируют на свои информационные входы лишь при наличии специального
разрешающего сигнала, называемого синхросигналом. Если синхросигнал неактивен,
то изменения состояний информационных входов не приводят к изменению состояния
триггера. Такие триггеры, в свою очередь можно разделить ещё на 4 группы по активному
состоянию синхровхода – запись информации в триггер может осуществляться при лог.
0/1 на синхровходе (срабатывание
по уровню), либо при нарастающем/спадающем фронтах
(срабатывание по фронту) этого сигнала. Часто говорят проще – по фронту или по
спаду сигнала.
Триггеры со
срабатыванием по уровню также иногда называют прозрачными (т.к. при активном
уровне синхросигнала они превращаются в повторитель), а триггеры, срабатывающие
по фронту – динамическими.
Рассмотрим
теперь некоторые типы триггеров (RS, D, T, JK) их
синтез.
2.1 Асинхронный RS триггер
RS триггер имеет 2 входа – R (Reset, сброс) и S (Set, установка). При RS=00 триггер не меняет своего
состояния (режим хранения), RS=01 – на прямом выходе триггера
устанавливается 1 (Q:=1), RS=10 – Q:=0. Сочетание RS=11 является нерабочим
(запрещённым). В том смысле, что на выходе может появиться как 0, так и 1, в
зависимости от внутренней схемотехники триггера. Более того, разные реализации RS триггера могут вести себя по-разному в такой ситуации.
Довольно часто
встречается R S триггер, т.е. установка происходит при S=0, сброс при R=0, хранение R S=11. Запрещённая комбинация R S=00.
RS триггер синтезируется как обычная КС. Таблица истинности:
Rt
St
Qt+1
0
0
Qt
0
1
1
1
0
1
1
1
*
Расширенная
(полная) ТИ:
Rt
St
Qt
Qt+1
0
0
0
0
0
0
1
1
0
1
0
1
0
1
1
1
1
0
0
0
1
0
1
0
1
1
0
*
1
1
1
*
Здесь Rt , St и Qt —
состояния сигналов R, S, Q в текущий момент времени, Qt+1 — состояние
выхода Q в следующий момент времени.
* — неопределённое (любое) состояние
По ТИ можно составить
карту Карно – рис. 13.
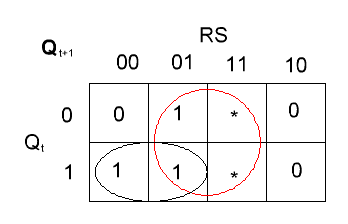
Рис 13. Карта Карно
для RS-триггера
Формула: Qt+1=Qt R + S.
Тождественные преобразования:
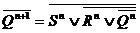
Схемные
реализации триггера – рис 14.
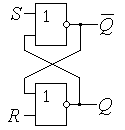
а)
б)
Рис. 14. Схемы RS и R S триггеров.
Следует
отметить, что в этих реализациях появление на входах запрещённой комбинации RS==1 для схемы на рис. 14-а ведёт к появлению нуля на обоих
выходах триггера. Для схемы на рис. 14-б запрещённая комбинация R S=00 приведёт к появлению единицы на обоих выходах. И то, и другое противоречит логике работы
триггера.
Таких ситуаций
всегда следует избегать при проектировании схем, содержащих RS триггеры любых модификаций.
УГО (условно-графическое
обозначение) RS-триггера – рис. 15.
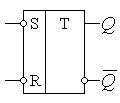
Рис. 15. УГО RS-триггера
Сами по себе RS-триггеры применяются достаточно редко, но они очень часто
являются основой для триггеров других типов.
2.2 Синхронный RS-триггер
Это, по сути
тот же RS триггер, но с синхровходом. Его можно
синтезировать также как и RS-триггер, через ТИ, карты
Карно и тождественные преобразования формул, но можно сразу добавить в схемы
рис. 8 пару элементов 2И либо 2И-НЕ – рис. 16.
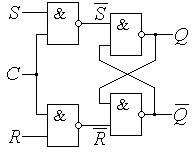
а)
б)
Рис. 16. Схемы
синхронного RS-триггера
Эти триггеры
будут реагировать на сигналы R, S лишь когда
синхросигнал C=1.
Если в схеме
рис 10-б использовать элементы 3И-НЕ, то мы получим т.н. синхронно-асинхронный RS-триггер – рис 17.
Рис. 17.
Синхронно-асинхронный RS-триггер.
Следует
отметить, что состояние входа C не влияет на входы R и S, поэтому их приоритет всегда выше синхронных входов R и S.
2.3 Асинхронный D-триггер
Асинхронный D-триггер – одновходовый триггер, т.е. у него есть лишь
один вход D. Его функция описывается формулой Qt+1 = Dt. Такой триггер
почти лишён какого-то практического смысла, единственное его назначение –
некоторая задержка сигнала. В простейшем случае его вообще не нужно синтезировать,
достаточно поставить любое чётное кол-во инверторов, включённых
последовательно.
2.3 Синхронный D-триггер
Гораздо
больший практический смысл и применение находит синхронный D-триггер.
Он имеет 2 входа – информационный D вход и синхровход C.
Упрощённая таблица
истинности имеет вид:
Ct
Dt
Qt
0
*
Qt+1
1
0
0
1
1
1
При C=0 триггер реализует режим хранения, С=1 – режим записи
информации.
Такой триггер
ещё называют защёлкой данных.
Синтезировать D-триггер можно как обычно, но можно использовать уже
синтезированный выше RS триггер, в итоге получится
схема – рис. 18 а.
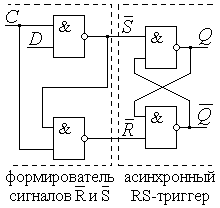
а)
б)
Рис. 18. Схема и УГО
синхронного D-триггера
Промышленность
выпускает микросхему К155ТМ2, содержащую 2 синхронных D-триггера,
которые имеют дополнительные входы R, S.
D-триггеры широко используются для создания других типов
триггеров (см. ниже) и для построения простых запоминающих устройств – регистров
и статических ОЗУ небольшой ёмкости (см. раздел 3).
2.3 Счётный T-триггер
Счётный T-триггер имеет один вход, при появлении на котором активного
уровня триггер меняет своё состояние на противоположное. Т.е. его функция
описывается формулой Qt+1=TQt + TQt
Синтезировать
можно как обычно, через ТИ, но проще использовать уже «имеющиеся в
распоряжении» синхронные RS и D-триггеры
— рис. 19.
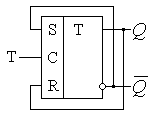
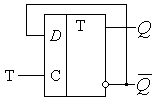
Рис. 19. Счётный T-триггер на базе синхронных RS и D триггеров
Легко заметить
недостаток обеих схем – если активный уровень T=1 будет
действовать на входе дольше времени срабатывания триггера, то триггер
самовозбудится – выходы будут непрерывно менять своё состояние на противоположное.
Т.е. получится генератор.
Для
преодоления этого недостатка счётные триггеры строят на базе 2-х триггеров и
инвертора, запись информации в которые происходит по противоположным уровням
входного сигнала – рис. 20.
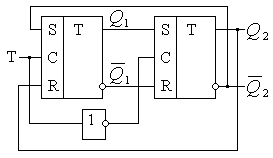
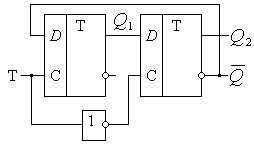
Рис. 20. Двухтактные
счётные триггеры.
Такие счётные
триггеры называют 2-хтактными.
Как можно
понять из схемы, при «зависании» счётного входа в любом состоянии сработает
лишь один триггер, состояние второго никак не изменится и генерации не
возникнет.
Счётные
триггеры имеют свойство делить частоту входного сигнала на 2 – рис. 21.
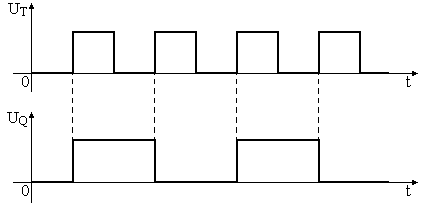
Рис. 21. Временная
диаграмма работы T-триггера
Такие триггеры
часто используются при построении счётчиков и делителей частоты (см. часть 2).
2.4 JK-триггер
JK-триггер является некой функциональной комбинацией RS и Т-триггеров.
Он имеет 2
входа – J и K (отсюда его
название), являющиеся прямыми аналогами входов S и R RS триггера. Отличие от RS-триггера
состоит в том, что запрещённая для RS триггере
комбинация RS=11 (JK=11) у JK-триггера приводит в переключению его выхода в
противоположное состояние (T-триггер). Т.о. запрещённых
комбинаций входов у JK-триггера нет.
JK-триггер описывается функцией Qt+1=KtQt + JtQt
Синтез можно
проводить как обычно, но проще составить это триггер из различных RS-триггеров – рис. 22.
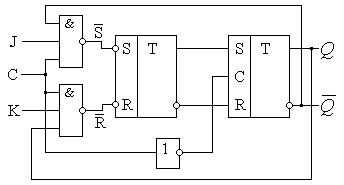
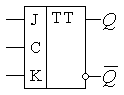
Рис. 22. Схема JK триггера и его УГО
Как можно
заметить из схемы, JK триггер всегда является
синхронным и 2-тактным.
JK является универсальным триггером – на его основе можно создать
любой другой триггер:
1. Про прямую
аналогию RS-триггеру было сказано выше. Точнее JK-триггер – аналог синхронного RSC-триггера;
2. Если подать J=D, а K=D, то мы получим D-триггер;
3. Для
получения T-триггера можно либо подать сигнал T одновременно на J и K, а C не использовать, либо подать J=K=1, а T подать на C.
Эти варианты
показаны на рис. 23.
Рис. 23. Схемы различных
триггеров на базе JK-триггера
JK-триггеры выпускаются промышленно (например, К155ТВ1).
В завершение
этого раздела необходимо сказать, что все рассмотренные триггеры срабатывают по
уровню (C=1) и для их нормального функционирования необходимо,
чтобы управляющие сигналы не изменялись пока C=1.
Исключение составляет лишь T-триггер (вообще не имеющий
инф. входа) и 2-тактный JK-триггер.
На практике это
условие фактически невыполнимое, поэтому почти все реальные триггеры (например,
К155ТМ2) используют т.н. динамическое управление. Т.е. триггеры срабатывают по
какому-либо фронту, а не по уровню, хотя есть и такие. На УГО входы C со срабатыванием по фронту обозначаются наклонной
чёрточкой, либо стрелкой – рис. 24.
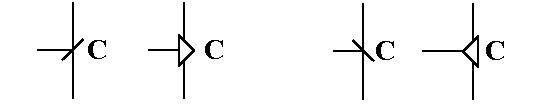
а)
б)
Рис. 24. Обозначение
синхровхода со срабатыванием по фронту: а – по нарастанию, б – по спаду сигнала
На практике, синхросигнал
называют тактовым сигналом.
Хотелось бы
отметить, что случай рис. 24-а также называют «рабочая отрицательная полярность
импульса», а 24-б – «рабочая положительная полярность импульса».
По мнению
автора, такие термины являются «пережитками прошлого» и очень редко
соответствуют действительности (применительно к современным микросхемам). Они часто
сбивают новичков с толку, поскольку не имеют ни малейшего отношения к
полярности напряжения, прикладываемого ко входу лог. схемы или
к полярности напряжения на её выходе.
Полярность
напряжения на входах-выходах лог. схем практически никогда не меняется и в подавляющем
большинстве случаев является положительной. Более того, простые цифровые
микросхемы редко защищены от переполюсовки сигнала либо питающего напряжения и,
если это случится, могут достаточно быстро выйти из строя.
Существуют,
конечно, схемы с изменяемой полярностью напряжения на входах-выходах, но это
уже, как правило, специализированные микросхемы-преобразователи уровней
напряжения (например, преобразователь уровней типа MAX232 для COM-порта ПК) или что-то родственное. В этой статье
речь о них не идёт.
2.5 Триггер Шмитта
Триггер Шмитта
– не является триггером в прямом понимании этого слова. Строго говоря, это даже
не цифровой элемент, а аналого-цифровой.
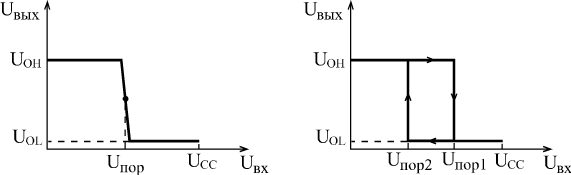
а)
б)
Рис. 25. Передаточная
характеристика инвертора (а) и триггера Шмитта (б)
Из рис. 25
видно, что триггер Шмитта похож на инвертор, но с петлёй гистерезиса. Т.е. если
входной сигнал будет колебаться в районе Uпор1-Uпор2, то выходное состояние триггера не меняется (некий
режим хранения).
Такие триггеры
не синтезируются из логических элементов, подобно всем остальным триггерам, а
создаются на базе операционных усилителей, либо из инверторов с резистивными
обратными связями.
Триггеры
Шмитта применяются не для хранения какой-то информации. Основная сфера и цель
их применения – выделение прямоугольных сигналов из каких-то зашумлённых линий
связи – рис 26.
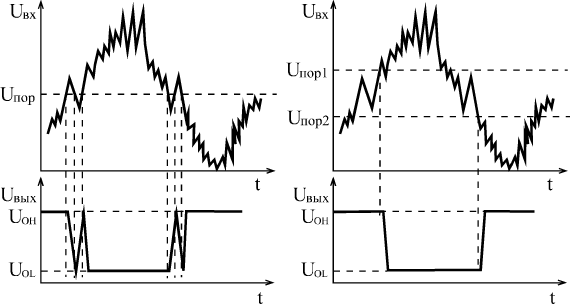
а) б)
Рис. 26. Реакция на зашумлённый и искажённый сигнал
инвертора (а) и триггера Шмитта (б)
Триггеры Шмитта
также применяются в схемах подавления дребезга кнопок – рис 27.
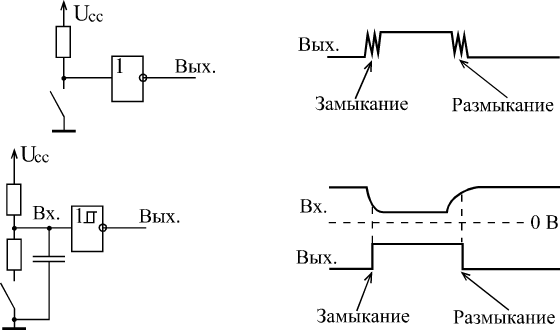
Рис. 27. Поведение инвертора
и триггера Шмитта в схеме с кнопкой
Литература, ссылки:
1. Бирюков С.А. Применение ИМС
серий ТТЛ. Москва, изд. «Патриот» совместно с ред.
журнала «Радио», 1992 г.
Автор: Павел Негробов (hd44780)