Управляющие автоматы. Принцип микропрограммного управления
Введение
Любое
устройство можно структурно разделить на управляющую часть и исполнительную. Управляющая
часть (управляющий автомат, УА) отвечает за взаимодействие с внешней средой, а
исполнительная (операционный автомат, ОА) – за выполнение каких-то действий.
На примере
простой ёлочной гирлянды – лампочки – исполнительная часть, а микросхему,
которая ими управляет – управляющая.
В простейшем
случае, УА может представлять собой соединённые последовательно генератор
низкой частоты (0.5-2 Гц), двоичный счётчик и дешифратор – рис. 1.
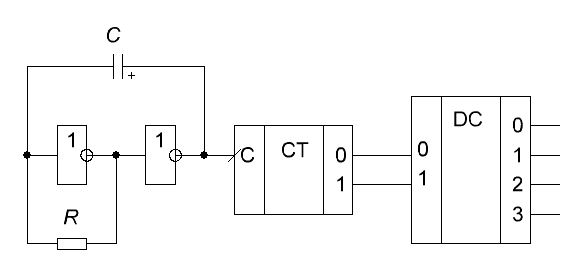
Рис. 1. Простейший УА
В этом случае,
на выходе дешифратора будет появляться бегущая единица. Можно также подключить
лампы непосредственно к выходам счётчика и т.д.
Из схемы понятны
аспекты работы этого УУ:
частотой генератора.
определяется алгоритмами работы счётчика и дешифратора.
Недостатки
тоже очевидны:
1. Невозможность какого-либо внешнего управления работой УУ. Управлять
можно лишь частотой генератора и параметрами импульсов (если взять генератор
«получше»). Алгоритмы работы счётчика и дешифратора вообще жёстко фиксированы,
т.к. это стандартные узлы со стандартным «поведением» и т.д.
2. Если мы захотим включать лампочки как-то иначе, например в порядке 0, 2,
1, 3, (или вообще «на лету» менять каким-либо образом эту очерёдность) либо
включать их парами (например, 0-1, 2-3), то окажется, что этого в принципе сделать
нельзя, т.к. счётчик/дешифратор или какие-то другие стандартные элементы «не
умеют» так работать.
Ну и т.д и т.п.
Для
преодоления этих недостатков разрабатывают специальные УА.
Раздел 1.
Управляющие автоматы с жёсткой логикой
Теория
управляющих абстрактных и конечных автоматов – очень обширная наука,
описывающая понятие автоматов, их поведение, формализацию, различные модели и
пр. Здесь не будут рассматриваться все эти теоретические аспекты, рассмотрим
лишь две практических варианта УА с жёсткой логикой.
Название «автомат
с жёсткой логикой» проистекает из того, что алгоритм функционирования такого
автомата жёстко задан его схемой. Для внесения даже незначительных изменений в
алгоритм необходимо полностью (или почти полностью) пересинтезировать всю схему
автомата. «Отделаться» какими-то мелкими изменениями возможно далеко не всегда.
Обобщённая
структурная схема УА с жёсткой логикой имеет вид – рис. 2.

Рис. 2. Обобщённая
структурная схема УА с жёсткой логикой
На рис. 2: X – множество входных сигналов автомата, Y – множество выходных сигналов, D – сигналы
управления памятью, T – сигналы состояния.
УА состоит из
2-х функциональных блоков:
1. КС –
комбинационная схема, формирующая выходные сигналы автомата и сигналы
управления памятью.
2. Память
автомата – просто набор триггеров (регистр). Кол-во триггеров n определяется кол-вом k требуемых состояний автомата. k определяется по-разному для разных автоматов. k равно ближайшему целому (в большую сторону) числу из
значений выражения 2n. Т.е. n=]log2k[. К примеру,
если у нас 5 состояний, то мы должны поставить 3 триггера (23=8>5), а если 8, то 4 (24=16>8).
Функционирование
УА может задаваться графом переходов либо таблицами истинности. Можно описать
его поведение и формулами: Y=ƒ1(X,T), D=ƒ2(X,T).
Очевидно, что при
использовании одновходовых триггеров (D и Т) КС
получается проще (для каждого триггера формировать надо лишь один сигнал
вместо 2, как для RS или JK триггеров).
На практике, если, например, в наличии есть лишь RS-триггеры,
то можно несколько «схитрить», сделав D-триггеры из RS и синтезировать КС в расчёте на D.
Следует также
отметить, что всегда следует применять триггеры с синхронизацией. Если использовать
триггеры без синхронизации, например, асинхронные RS-триггеры,
то полученный автомат будет «перещёлкивать» все свои состояния очень быстро, со
скоростью, определяемой скоростью работы элементов, входящих в КС и самих
триггеров. Кроме того, на выходе могут появляться какие-то другие, случайные и
«незапланированные» комбинации состояний выходов.
Если
применяются D-триггеры, то можно использовать обычные
регистры хранения вместо раздельных триггеров. Это может существенно упростить конечную
схему.
УА с жёсткой
логикой бывают 2-х видов – Мили и Мура.
1.1 Управляющий
автомат Мили
Автомат Мили имеет
структуру, на 100% совпадающую с рис. 2. И поведение его описывается теми же
общими формулами – Y=ƒ1(X,T), D=ƒ2(X,T). Потому иногда говорят, что этот
автомат генерирует (в смысле изменяет) выходные сигналы при переходах из одного
состояния в другое. Здесь подчёркивается тот факт, что Y непосредственно
зависит от X.
Рассмотрим
синтез автомата Мили на примере.
Допустим, нам
необходимо построить автомат, имеющий 2 входных сигнала (x1,
x2) и 4 выходных (y1-y4):
x1
x2
y1
y2
y3
y4
0
1
1
0
1
1
1
1
0
0
0
1
1
0
0
1
1
1
1
1
0
0
0
0
0
0
1
1
1
1
0
1
0
1
1
1
Т.к. мы имеем
6 состояний, то нам понадобится 3 триггера. Используем для простоты D-триггеры. Построим теперь полную таблицу истинности
автомата:
Сост.
T1
T2
T3
x1
x2
y1
y2
y3
y4
D1
D2
D3
0
0
0
0
0
1
1
0
1
1
0
0
1
1
0
0
1
1
1
0
0
0
1
1
0
0
2
1
0
0
1
0
0
1
1
1
1
1
1
3
1
1
1
1
1
0
0
0
0
1
1
0
4
1
1
0
0
0
1
1
1
1
0
1
1
5
0
1
1
0
1
0
1
1
1
0
0
0
Здесь мы:
автомата.
автомата сигналами текущего состояния триггеров Tx.
Кодировать можно как угодно, единственное требование – все коды состояний
д.б. уникальны. Т.е. не должно быть 2-х и более состояний с одинаковыми
кодами.
сигналами Tx и сигналами Dx управления триггерами для того, чтобы автомат мог
переходить из одного состояния в другое.
Также
подразумевается, что состояния меняются по кругу. В разделе 1.2 показано, как
реализовывается переход их одного состояния в 2 других в зависимости от разных
входных сигналов.
По этой
таблице уже можно синтезировать КС автомата. Но перед тем, как перейти
непосредственно к синтезу, отметим небольшую особенность использованного
кодирования состояний: сигнал T1 повторяет x1 со сдвигом на один такт. Это позволяет не строить какие-то
формулы и схемы для сигнала D1, а сразу пустить x1 на D1. Подобные «уловки» в ряде
случаев позволяют упростить схему и ускорить её быстродействие.
КС должна
формировать 7 сигналов: y1-y4 и D1-D3. Составим формулы для каждого сигнала:

По формулам
можно нарисовать схему автомата. Мы этого делать не будем, здесь и так всё
понятно.
Следует
отметить, что у автомата Мили теоретически возможна ситуация, при которой
окажется, что какой-то yi зависит лишь от xj и не зависит от Tn. Т.е. автомат изменяет выходные
сигналы, не изменяя своего состояния. Учесть это при синтезе сложно, гораздо
проще после него ввести какие-то «ненужные» зависимости yi от
каких-то Tn.
1.2 Управляющий
автомат Мура
Автомат Мура
отличается от Мили тем, что он описывается формулами Y=ƒ1(T), D=ƒ2(X,T). Т.е. его выходные
сигналы зависят лишь от состояния триггеров. Потому его КС фактически
распадается на 2 независимые КС – рис. 3.
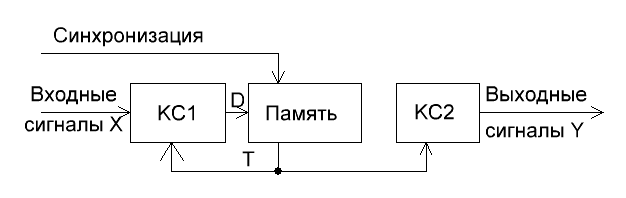
Рис. 3 Структура
автомата Мура
КС1 реализует
функцию D=ƒ2(X,T),
а КС2 — Y=ƒ1(T).
Построим
автомат Мура для того же примера:
Сост.
x1
x2
y1
y2
y3
y4
0
0
1
1
0
1
1
1
1
1
0
0
0
1
2
1
0
0
1
1
1
3
1
1
0
0
0
0
4
0
0
1
1
1
1
5
0
1
0
1
1
1
Сразу отметим,
что состояния 2 и 5 для Мура полностью эквивалентны, т.к. они генерируют
идентичные наборы выходных сигналов. Потому состояние 5 можно выбросить и
добавить дополнительный переход из состояния 2 по сигналам x1x2=01 в состояние 0. Это действие заменит выброшенное 5-е состояние в плане
переходов.
Исключение эквивалентных
состояний в общем случае может сократить число триггеров автомата.
ТИ для КС1
(таблица переходов автомата):
Сост.
T1
T2
T3
X1
x2
D1
D2
D3
0
0
0
0
0
1
0
1
1
1
0
1
1
1
1
1
1
0
2a
1
1
0
1
1
1
1
1
2b (5)
1
1
0
0
0
0
0
0
3
1
1
1
1
1
1
1
0
4
0
1
0
0
0
0
1
1
Правила
кодирования состояний те же, что и автомате Мили.
Коды состояний
001, 100, 101 и сочетание входных сигналов x1x2=10 не используются, это можно учитывать при
минимизации.
Обратите
внимание, что в таблице 2 строки, соответствующие состоянию 2. Строка 2b соответствует выброшенному состоянию 5. Видно,
что из неё автомат переходит в состояние 0.
Получим
минимальные формулы сигналов D1, D2 и D3 КС1:
Карта Карно
для сигнала X1 – рис 4.
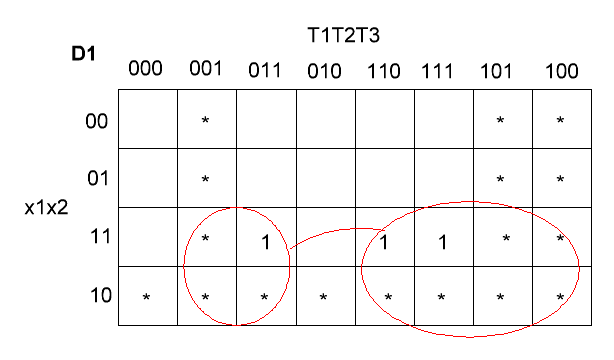
Рис 4. Карта Карно
для сигнала X1.
Из карты следует,
что D1 = x1. Это же видно из ТИ.
Аналогично:
D2 = x1 + T2 + T1 T2 T3 x2
D3 = T1 T2 T3 x2 + T2 + T1 T2 T3 x1
ТИ для КС2
автомата:
Сост.
T1
T2
T3
y1
y2
y3
y4
0
0
0
0
1
0
1
1
1
0
1
1
0
0
0
1
2
1
1
0
0
1
1
1
3
1
1
1
0
0
0
0
4
0
1
0
1
1
1
1
Сигналы:
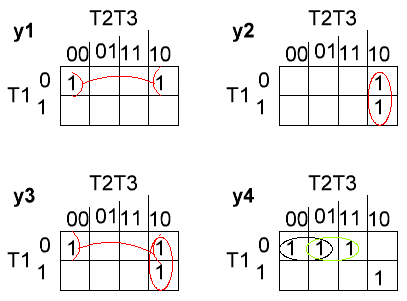
Рис.5 Карты Карно для
сигналов y1-y4
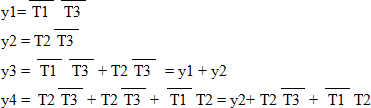
Из анализа
формул видно, что y3 и y4 можно
формировать, используя уже готовые y1 и y2. Это может дополнительно упростить КС2, но на практике
такое решение снижает нагрузочную способность схемы на выходах y1 и y2.
Также, можно
упростить реальную схему, если в каком-то смысле объединять схемы КС1 и КС2,
формируя общие для них внутренние сигналы (например, T1 T3) и использовать их одновременно в обоих схемах. Конечно, обращая внимание на длину
получаемых цепочек элементов и на их быстродействие (при увеличении длины
цепочки падает её быстродействие).
Даже несмотря
на то, что при рассмотрении автомата Мили мы не минимизировали его формулы,
можно заметить, что автомат Мура проще уже потому, что для формирования Y не нужны сигналы X.
Раздел 2.
Микропрограммное управление.
Основное
достоинство рассмотренных УА с жёсткой логикой – их высокое быстродействие,
определяемой быстродействием используемой элементной базы.
Но есть и
большие недостатки:
1. при необходимости внесения любых, даже небольших изменений алгоритма
работы схему автомата надо полностью пересинтезировать.
2. при большом числе входных и выходных сигналов схема автомата сильно
разрастается, а синтез становится сложным и тяжёлым занятием. Так, карты Карно
уже при 5 аргументах (см. рис. 4) становятся трудночитаемыми и
труднопонимаемыми, т.к. не все клетки, которые можно склеить и минимизировать,
являются физически соседними. Неизбежным итогом этого может стать неполная
минимизация и, как следствие излишне сложная и избыточная схема полученного
автомата. На работоспособность схемы это, правда, не повлияет.
Второй
недостаток особенно ярко проявляется при разработке различных вычислительных
структур (часть 4), где есть много операционных узлов, для которых требуется
очень много выходных сигналов и много состояний управляющего автомата.
В таких
случаях используют принципиально другие УА – УА с микропрограммным управлением.
Структура
такого УА изображена на рис. 6.
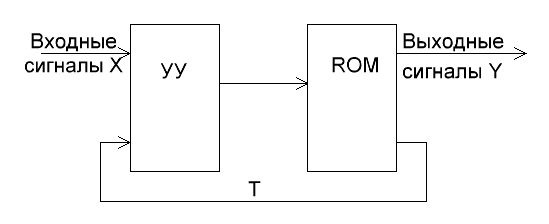
Рис. 6. Структура УА
с микропрограммным управлением
Основа такого
управляющего аппарата – ROM – ПЗУ. Каждая ячейка ПЗУ
хранит микрокоманду (МК) – набор выходных сигналов Y для каждого состояния автомата и набор управляющих сигналов T для своего сугубо внутреннего устройства управления УУ.
В плане
генерации выходных сигналов все микропрограммные автоматы идентичны автомату
Мура – Y зависят лишь от состояния памяти автомата.
УА с
микропрограммным управлением бывают 2-х типов – с естественной адресацией микрокоманд
и с принудительной. В каждом случае структура УУ разная.
Рассмотрим эти
2 варианта.
2.1. Микропрограммный
УА с принудительной адресацией
Структура УА с
принудительной адресацией приведена на рис. 7.

Рис. 7. Структура УА
с принудительной адресацией
На рис.7: MS1 – мультиплексор
входных сигналов, MS2 – мультиплексор адреса
микрокоманды, РАМК – регистр адреса микрокоманды, МПЗУ – ROM микропрограмм из рис. 6, РМК – регистр микрокоманд.
Разрядность MS2 и РАМК равна адресности ROM n=]log2k[, где k – кол-во
микрокоманд автомата. К примеру, если у нас 13 микрокоманд, то для них надо 13
ячеек ПЗУ, для адресации которых требуется n=]log213[=4 разряда адреса.
Разрядность
ПЗУ и РМК равна кол-ву всех сигналов, которое должна выдавать ROM
Формат РМК
идентичен формату микрокоманды: A0 и A1
– адрес следующей МК в ПЗУ, по которому перейдёт автомат, если
выбранный управляющий сигнал равен 0 или 1 соответственно. Nx
– код входного сигнала, проверяемого в текущей МК, ОЧ – операционная
часть, содержит все выходные сигналы автомата.
ДШМО –
дешифратор микрооперации. Его назначение – уменьшить разрядность ПЗУ и РАМК, в
том случае, если все или часть входных сигналов Y являются
унитарными и их можно закодировать таким образом, чтобы разрядность поля ОЧ
была меньше кол-ва выходных сигналов. В общем случае он не нужен.
В реальности
регистр РМК можно исключить, т.к. ПЗУ не меняют состояния своих выходов при
неизменности адреса. Т.е., пока содержимое РАМК неизменно, то и на выходах ПЗУ будет
неизменная информация.
Целесообразность
использования ДШМО на практике зависит и от разрядности реальных ПЗУ, из
которых будет строиться МПЗУ автомата.
Так, например,
если мы будем использовать 8-разрядные ПЗУ, то, понятно, что конечная
разрядность МПЗУ будет кратна 8 битам. Потому, если, допустим, на все поля в
сумме без доп. кодирования Y понадобится 15 разрядов, а
с кодированием 12, то доп. кодирование каких-то Yi и
введение дешифратора не приведёт к уменьшению конечного МПЗУ (и на 15 и на 12
сигналов надо 2 8-битных микросхемы ПЗУ), а дополнительный дешифратор лишь
усложнит схему и, возможно, снизит её быстродействие. Но, если в распоряжении
есть и 8 и 4-разрядные ПЗУ (8+4=12), то в случае с 12-разрядной МК мы можем
применить не две 8-битные микросхемы, а одну 8 и одну 4 битную, то вариант с ДШ
может оказаться выгоднее.
Также, следует
отметить, что промышленность не выпускает регистров с двумя входными шинами
(РАМК на рис. 7). Потому, при необходимости такой узел м.б. заменён
многоразрядным мультиплексором с 2-х направлений и обычным одновходовым
регистром.
Рассмотрим
подробно работу микропрограммного автомата с принудительной адресацией.
Работа автомата
начинается с занесения в регистр адреса микрокоманд (РАМК) кода операции (по
сути стартового адреса микрокоманды). В простейшем случае вместо занесения
адреса можно использовать вход сброса регистра.
На время
исполнения микрокоманда из RAM копируется в регистр
микрокоманд РМК.
Далее мультиплексор MS1 передаёт на свой выход значение входного сигнала Xi, указанного полем Nx микрокоманды.
По сигналу с MS1 мультиплексор MS2 выбирает один из 2-х адресов A0/А1
и передаёт его на вход РАМК.
После этого
всё повторяется.
Отметим, что
на первый (с номером 0) вход мультиплексора MS1 заведен
постоянный лог. 0. Это даёт возможность реализации МК с безусловным переходом
по адресу A0 в тех МК, где не нужно проверять никакие
входные сигналы. Вместо лог. 0 можно использовать лог. 1. Это повлияет лишь
на то, что адресом перехода будет считаться содержимое поля A1,
а не A0.
Наличие MS1 обусловливает следующую особенность автомата – любая МК
может проверять (учитывать) лишь один сигнал Xi. Это
обстоятельство относится к любым автоматам с микропрограммным управлением (не
лишь с принудительной адресацией). Потому, если в какой-либо МК необходимо
проверять несколько Xi, то такая МК разбивается на
несколько, проверяющих требуемые Xi в произвольном
порядке.
В ряде случаев,
если входных сигналов не очень много, то, в принципе, можно заменить
мультиплексор MS1 простой схемой совпадения кодов, а в
МК вместо Nx записывать требуемое
сочетание Xi.
В качестве
примера рассмотрим микропрограммную реализацию того же автомата, который мы
рассматривали для моделей Мили и Мура.
Напомним его
ТИ:
Сост.
x1
x2
y1
y2
y3
y4
0
0
1
1
0
1
1
1
1
1
0
0
0
1
2
1
0
0
1
1
1
3
1
1
0
0
0
0
4
0
0
1
1
1
1
5
0
1
0
1
1
1
Сначала нам
необходимо закодировать входные сигналы автомата x1, x2 и постоянный лог. 0 на нулевом входе мультиплексора MS1:
Вход
Поле Nx микрокоманды
0 (лог. 0)
00
1 (x1)
01
2
(x2)
10
Микропрограмма
(МП) автомата будет иметь вид:
Адрес МК (состояние)
A0
A1
Nx (Xi)
Y={y1,y2,y3,y4}
0000 (сост. 0а)
0001
0000
01 (x1)
1011
0001 (сост. 0б)
0000
0001
10
(x2)
1011
0010 (сост. 1а)
0010
0011
01
(x1)
0001
0011 (сост. 1б)
0011
0100
10
(x2)
0001
0100 (сост. 2а)
0100
0101
01
(x1)
0111
0101 (сост. 2б)
0110
0101
10 (x2)
0111
0110 (сост. 3а)
0110
0111
01
(x1)
0000
0111 (сост. 3б)
0111
1000
10
(x2)
0000
1000 (сост. 4а)
1001
1000
01
(x1)
1111
1001 (сост. 4б)
1010
1001
10
(x2)
1111
1010 (сост. 5а)
1011
1010
01 (x1)
0111
1011 (сост. 5б)
1011
0000
10
(x2)
0111
Таким образом,
требуемая адресность ПЗУ равна 4 (4-разрядный адрес), а его разрядность равна 4+4+2+4
= 14. Ёмкость ПЗУ составит 16 ячеек, из которых мы займём 12.
Отметим
следующие особенности:
1. Кол-во
состояний автомата удвоилось, т.к. микропрограммные автоматы описываемой
архитектуры не могут реагировать в одном состоянии сразу на несколько входных
сигналов. Но, если бы мы имели в ТИ автомата следующую строку:
Сост.
x1
x2
y1
y2
y3
y4
5
*
1
0
1
1
1
то при разработке МП мы могли бы
обойтись одним состоянием:
1010 (сост. 5)
1010
0000
10 (x2)
0111
2. Сигнал лог.
0 (Nx==0) нам здесь не понадобился. Для иллюстрации его
использования представим себе, что в ТИ есть такая строка:
Сост.
x1
X2
y1
y2
y3
y4
6
*
*
0
1
1
1
7
0
*
1
0
1
1
Т.е. из
состояния 6 мы всегда переходим в состояние 7.
В этом случае
в МП мы можем написать:
Адрес МК (состояние)
A0
A1
Nx (Xi)
Y={y1,y2,y3,y4}
1100 (сост. 6)
1101
0000
00 (лог. 0)
0111
1101 (сост. 7)
0000
1101
01 (x1)
1011
Как видно, в
состоянии 6 автомат не будет проверять никакие Xi, а
просто перейдёт из него в состояние 7.
3. Таблица МП
представляет собой так называемую «прошивку» автомата, она полностью описывает содержимое ROM автомата: 1-й столбец – адрес МК в ПЗУ, 4 остальных
– сами МК (содержимое ПЗУ). Она на 100% задаёт его алгоритм работы.
Из
практического примера виден один общий недостаток МП автоматов – из-за
невозможности проверить несколько Xi одновременно,
кол-во состояний (микрокоманд) МП автомата всегда больше кол-ва состояний эквивалентного
автомата Мура (или Мили). Соответственно, и его быстродействие ниже – тем дольше,
чем больше входных сигналов нужно обработать в одном состоянии эквивалентного
автомата с жёсткой логикой.
Но т.к. современные
микросхемы ПЗУ имеют достаточно большие ёмкости, то этот недостаток несущественен
на фоне огромного преимущества, заключающегося в том, что если нам понадобится
как-то изменить алгоритм функционирования автомата, то нам достаточно «подправить»
микропрограмму и перепрошить (изменить содержимое) ПЗУ. Аналогичная задача для
автоматов с жёсткой логикой потребует повторного полного цикла разработки схемы
автомата «с нуля».
2.2. Микропрограммный
УА с естественной адресацией
Структура,
предлагаемая в аппарате с принудительной адресацией, удобна, но можно заметить,
что большинство МК в ПЗУ идут подряд, а те, которые не подчиняются этому
правилу, нередко можно переставлять местами. Это относится к состояниям «с
буквами» в предыдущем примере, когда автомат, фактически находясь в одном
состоянии, проверяет какой-то набор входных сигналов.
Потому
логично представить себе автомат, имеющий в своём составе вместо адресного
мультиплексора MS2 и регистра РАМК простой счётчик адреса
с возможностью предзагрузки, которой мы могли бы воспользоваться для выполнения
перехода в несмежное с текущим состояние.
Такие МП
автоматы называются автоматами с естественной адресацией – рис 8.
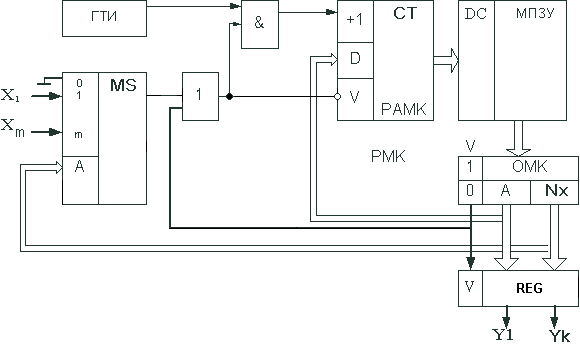
Рис 8. Структура МП
УА с естественной адресацией.
Можно
заметить, что здесь есть 2 вида микрокоманд (РМК на рисунке), различающихся
старшим битом V:
0 – ОМК –
операционная микрокоманда, содержащая во всех остальных разрядах сигналы Y.
1 – УМК – управляющая микрокоманда, т.е. МК перехода. Её поле A – адрес перехода, подаётся на входы предзагрузки
счётчика. Nx – то же, что и выше – код проверяемого
сигнала Xi. Безусловный переход реализуется подобно
первому варианту – фиксированным лог. 0 на одном из входов MS.
Т.е. автомат выполняет переход, если Xi==0.
Счётчик-РАМК
при V=0 выполняет загрузку со входов D, при V=1 выполняется счёт (инкремент – увеличение
значения на 1) по тактовым импульсам на входе +1.
В структуре
автомата также появился ещё один дополнительный регистр – REG. Его задача – сохранять выходные сигналы автомата, когда тот выполняет
команды переходов (V==1). При V==0 регистр
прозрачен, передаёт состояние входов на выходы. На выходе REG можно
ставить ДШМО, как в первом случае. Соображения по целесообразности его
установки совершенно те же, что и для принудительной адресации.
Функционирование
такого автомата несколько отличается от предыдущего варианта с принудительной
адресацией.
Если автомат
выполняет ОМК, то 1 из старшего бита МК блокирует мультиплексор входных
сигналов MS элементом ИЛИ и запрещает счётчику-РАМК
выполнять предзагрузку адреса перехода. Одновременно выходной регистр сохраняет
в себе выходные сигналы автомата. По приходу следующего тактового импульса
счётчик увеличится на 1, выбирая следующую МК.
Если
выполняется УМК, то выходной регистр блокируется сигналом V=0, а элемент ИЛИ разрешает прохождение сигнала мультиплексора. Далее, если Xi==0, то прохождение тактовых импульсов на счётчик
запрещается, но разрешается предзагрузка его значением пола A микрокоманды
– выполняется переход. Если Xi==1, то предзагрузка
запрещена, разрешен проход тактового импульса – перехода нет.
Рассмотрим
разработку МП для такого автомата на примере:
Сост.
x1
x2
y1
y2
y3
y4
0
0
1
1
0
1
1
1
1
1
0
0
0
1
2
1
0
0
1
1
1
3
1
1
0
0
0
0
4
0
0
1
1
1
1
5
0
1
0
1
1
1
6
*
*
0
1
1
1
7
0
*
1
0
1
1
Это тот же
пример, что и выше, но с двумя доп. состояниями 6 и 7.
Также, как и
раньше, нам сначала необходимо закодировать входные сигналы автомата x1, x2 и постоянный лог. 0 на нулевом
входе мультиплексора MS1:
Вход
Поле Nx микрокоманды
0 (лог. 0)
00
1 (x1)
01
2
(x2)
10
Затем
составляем микропрограмму автомата (прошивку ПЗУ):
Адрес МК (состояние)
V
МК
00000 (сост. 0а)
0 (ОМК)
Y=1011
00001 (сост. 0б)
1
(УМК)
Nx=10 (x2), A=00001
00001 (сост. 0в)
1
(УМК)
Nx=01 (x1), A=00011
00010 (сост. 0г)
1
(УМК)
Nx=00 (лог.
0), A=00001 – безусловный переход
00011 (сост. 1а)
0 (ОМК)
Y=0001
00100 (сост. 1б)
1
(УМК)
Nx=01 (x1), A=00100
00101 (сост. 1в)
1
(УМК)
Nx=10 (x2), A=00100
00110 (сост. 2а)
0 (ОМК)
Y=0111
00111 (сост. 2б)
1
(УМК)
Nx=01 (x1), A=00111
01000 (сост. 2в)
1
(УМК)
Nx=10 (x2), A=01011
01010 (сост. 2г)
1
(УМК)
Nx=00 (лог.
0), A=00111 – безусловный
переход
01011
(сост. 3а)
0 (ОМК)
Y=0000
01100
(сост. 3б)
1
(УМК)
Nx=01 (x1), A=01100
01101 (сост. 3в)
1
(УМК)
Nx=10 (x2), A=01100
01110 (сост. 4а)
0 (ОМК)
Y=1111
01111 (сост. 4б)
1
(УМК)
Nx=01 (x1), A=10001
10000 (сост. 4в)
1
(УМК)
Nx=00 (лог.
0), A=01111 – безусловный
переход
10001 (сост. 4г)
1
(УМК)
Nx=10 (x2), A=10011
10010 (сост. 4д)
1
(УМК)
Nx=00 (лог.
0), A=01111 – безусловный
переход
10011 (сост. 5а)
0 (ОМК)
Y=0111
10100 (сост. 5а)
1
(УМК)
Nx=10 (x2), A=10100
10101 (сост. 5б)
1
(УМК)
Nx=01 (x1), A=10111
10110 (сост. 5в)
1
(УМК)
Nx=00 (лог.
0), A=10100 – безусловный переход
10111 (сост. 6а)
0 (ОМК)
Y=0111
10111 (сост. 7а)
0 (ОМК)
Y=1011
10111 (сост. 7б)
1
(УМК)
Nx=01 (x1), A=00000
11000 (сост. 7в)
1
(УМК)
Nx=00 (лог.
0), A=10111 – безусловный переход
Требуемая
адресность ПЗУ равна 5 (5-разрядный адрес), а его разрядность равна 1 + max (4, 2 + 4) =1 + max
(4, 6) = 1+6=7.
Полная ёмкость
ПЗУ составит 32 ячейки, из которых мы заняли 27.
Отметим, что:
— кол-во
состояний автомата с естественной адресацией существенно больше кол-ва состояний
даже автомата с принудительной адресацией. Это вызвано невозможностью
непосредственного перехода при Xi==1, в таких ситуациях
необходимо сочетание условного и безусловного перехода.
— требуемая
разрядность ПЗУ меньше, чем для автомата с принудительной адресацией.
Адресность – наоборот.
Раздел 3. Выводы и
рекомендации
В этой части
были рассмотрены 4 классические архитектуры управляющих автоматов.
При выборе той
или иной архитектуры для того или иного случая следует помнить:
1. Абсолютно
любой УА реализуем на любой их 4-х архитектур. Весь вопрос заключается лишь в
выборе варианта, который даст наиболее простую схему и требуемые
эксплуатационные характеристики.
2. Для
относительно простых устройств, не требующих возможности какого-либо изменения
функционала можно использовать жёсткую логику, иначе – МП подход.
3. В общем
случае, естественная адресация выгоднее для автоматов с относительно большим
кол-вом выходных сигналов и малым выходных.
4. Окончательный
вывод о применении той или иной архитектуры всегда следует делать исходя из
имеющейся элементной базы и того, что необходимо получить в результате.
5. Можно
смешивать разные архитектуры УУ в составе одного устройства. К примеру, в
составе какого-то процессора управлять аппаратным умножителем чисел можно жёсткой
логикой (простые, стандартные, давно «обкатанные» алгоритмы, мало входных и
выходных сигналов), но при этом всё арифметико-логическое устройство (АЛУ)
будет управляться МП автоматом, т.к. это АЛУ имеет множество разных блоков.
Такой подход может существенно увеличить быстродействие всей схемы в целом.
И т.д.
Автор: Павел Негробов (hd44780)