Введение
Иногда возникают ситуации, когда в очередной радиолюбительской (и не лишь) конструкции необходимо применить нелинейный элемент. Передо мной такая задача возникла, когда я собирал цифровой люксметр из подручных средств. В качестве датчика освещённости был выбран фоторезистор. При помощи АЦП микроконтроллера мне нужно было замерять напряжение на фоторезисторе и выводить освещенность на экран. А как известно, фоторезистор — это полупроводниковый элемент, который изменяет своё сопротивление в зависимости от величины попадающего на него светового потока. И тут мне не повезло. Нужный мне для измерения диапазон освещенностей как раз находился на нелинейном участке характеристики этого фоторезистора. И тут на помощь пришёл метод, который называют «Кусочно линейная аппроксимация».
Кратко о методе
Аппроксима́ция (от лат. proxima – ближайшая) или приближе́ние — научный метод, состоящий в замене одних объектов другими, в каком-то смысле близкими к исходным, но более простыми.
Название метода говорит само за себя. Суть его состоит в том, что нелинейную функцию разбивают на несколько участков, каждый из которых заменяют линейной функцией (прямой, соответствующей закону y=kx), максимально приближённой к исходному «кусочку» нелинейной функции. Понятно, что узнать вторую координату точки линейной функции, зная первую координату, гораздо проще, чем высчитывать то же самое с нелинейной функцией, подчиняющейся непонятно какому закону.
Если пока что-то непонятно, не пугайтесь. Дальше всё будет разобрано на конкретном примере.
Пример использования метода

На рисунке 1 представлена схема, на которой Rx — некий нелинейный элемент, R1 — постоянный резистор сопротивлением 5 кОм. Напряжение
Uпит = 5 В. Предположим, что Rx изменяет своё сопротивление в зависимости от температуры. Эдакий особенный терморезистор. Нам необходимо измерять температуру от 0 до +110 градусов по шкале Цельсия. Из даташита на терморезистор или экспериментальным путем находим график зависимости сопротивления Rx от температуры. В нашем случае этот график представлен на рисунке 2.
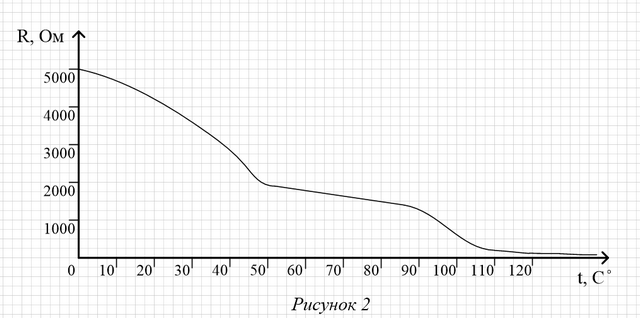
Видим, что при температуре в 0 градусов сопротивление терморезистора составляет 5000 Ом (5 кОм), а при температуре +110 градусов — около
250 Ом.
Если посмотреть на рисунок 1, то видно, что Rx и R1 включены последовательно и образуют делитель напряжения. Получается, что при температуре в 0 градусов напряжение Uвых будет равно 2.5 В (т.к. Rx будет равно R1). А при температуре в 110 градусов,
напряжение Uвых = Uпит * ( R1 / (R1+Rx) ) = 5 * ( 5000 / (5000 + 250) ) = 4.76 В.
Теперь наш график нужно разбить на несколько участков и на этих участках кусочки нелинейной функции нужно заменить линейными. Как это будет выглядеть показано на рисунке 3.
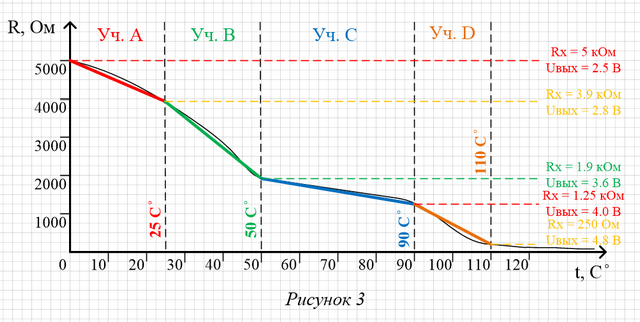
В результате разбивки графика получилось 4 участка — А, В, С, D. На рисунке справа для каждой получившейся крайней точки рассчитано значение сопротивления Rx (по графику) и Uвых (по формуле приведённой выше).
Теперь алгоритм программы, которая будет обрабатывать наше измеренное значение и переводить его из вольт в градусы, будет таким:
1. Определить, к какому из 4-х участков принадлежит полученное значение.
2. Исходя из п.1 выбрать формулу для расчёта температуры и выполнить расчёт.
3. Вывести результат вычислений
Определение формул для каждого участка
Каждый из участков характеризуется наклоном линии (S). Кстати говоря, на данном этапе вместо значений сопротивления Rx по оси Y можно подставить напряжения, которые мы посчитали для каждой общей точки (2.5, 2.8, 4.0, 4.8) или даже сразу значения АЦП. Поскольку АЦП выдает результат не в Вольтах, а в «условных единицах» (для 10-битного АЦП — от 0 до 1023), то нужно будет при помощи пропорции пересчитать напряжения Uвых в «условные единицы» АЦП. В данном примере я покажу расчёт в вольтах.
И так. Чтобы вычислить наклон линии на участке нужно разделить приращение по оси X на приращение по оси Y. Поясняю. Для участка А приращение по оси X = 25 — 0 = 25, а приращение по оси Y = 2.5 — 2.8 = — 0.3 (это в вольтах). Таким образом, наклон линии участка А равен:
S (A) = (25-0) / (2.5 — 2.8) = 25 / — 0.3 = — 83.3;
Предположим, результат измерения Uвых у нас составило 2.61 В. Чтобы вычислить температуру используем формулу:
t = ( (Uвых — Umin) * S) + dX;
dX — это смещение участка относительно нуля по оси X. Для участка А оно равно 0, потому что участок А начинается с 0. Для участка В оно равно 25, потому что участок В начинается с 25. Для участка D dX=90.
Umin — это напряжение нижней точки данного участка. Для А — 2.5 В, для В — 3.6 В, для С — 4.0 и т.д.
Таким образом, температура при напряжении Uвых = 2.61 В равна: t = ( (2.61 — 2.8) * (-83.3) ) + 0 = 15.82 С.
Для участка В:
Наклон: S (B) = (50 — 25) / (2.8 — 3.6) = 25 / — 0.8 = — 31.25
Смещение: dX (B) = 25
Нижняя точка: Umin (B) = 3.6 В
Если замер Uвых показал, 3.15 В, то t = ( (3.15 — 3.6) * (-31.25) ) + 25 = 39.0 С.
Таким же образом вычисляются данные для остальных участков.
Основные формулы
S = (X2 — X1) / (Y2 — Y1);
t = ( (Uвых — Umin) * S) + dX;
Об алгоритме программы
После замера АЦП и получения значения напряжения Uвых, программа должна определиться, как какому участку относится данное значение. Проще всего это реализовать при помощи условного оператора if. Выглядеть это будет примерно так:
if (Uвых >= 2.5 & Uвых <= 2.8) {Вычисляем t по формуле для участка А}
else if (Uвых > 2.8 & Uвых < 3.6) {Вычисляем t по формуле для участка В}
else if (Uвых >= 3.6 & Uвых < 4.0) {Вычисляем t по формуле для участка С}
else {Вычисляем t по формуле для участка D}
Вывод
Таким образом, получаем довольно эффективный метод для обработки нелинейных функций. При определенной сноровке применение этого метода занимает мало времени. Метод обеспечивает приемлемую точность для большинства любительских конструкций. Занимает намного меньше Flash-памяти, по сравнению, к примеру, если бы мы вручную высчитывали 1023 значения и заносили их в массив (создавали таблицу значений в памяти МК).